A Deep Dive into Policy Optimization Algorithms & Frameworks for Model Alignment

A Comprehensive Exploration of Policy Optimization Algorithms and Frameworks

Introduction

Reinforcement Learning (RL) is an intriguing area of machine learning that deals with the actions of intelligent agents within an environment to maximise cumulative rewards. Its prominence has surged in recent years due to its prowess in tackling complex issues.

 

When it comes to supervised learning using a static dataset like Wikimedia Commons, we can rely on running a stochastic gradient descent optimiser and expect our model to converge towards a satisfactory local optimum. However, the path to success in RL is far more complex. One of the key issues with RL is that the training data is dynamically generated based on the current policy. Unlike supervised learning where a fixed dataset is used, RL involves an agent interacting with its environment to create training data. Consequently, this leads to constantly changing data distributions for observations and rewards as the agent learns, introducing significant instability into the training process.

Moreover, RL faces challenges such as heightened sensitivity to hyperparameter tuning and initialisation settings. For instance, improper adjustments like setting a high learning rate could trigger policy updates that drive the network into regions of parameter space from which recovery may be difficult. This scenario results in subsequent data collection being conducted under sub-optimal policies, further complicating the learning process.

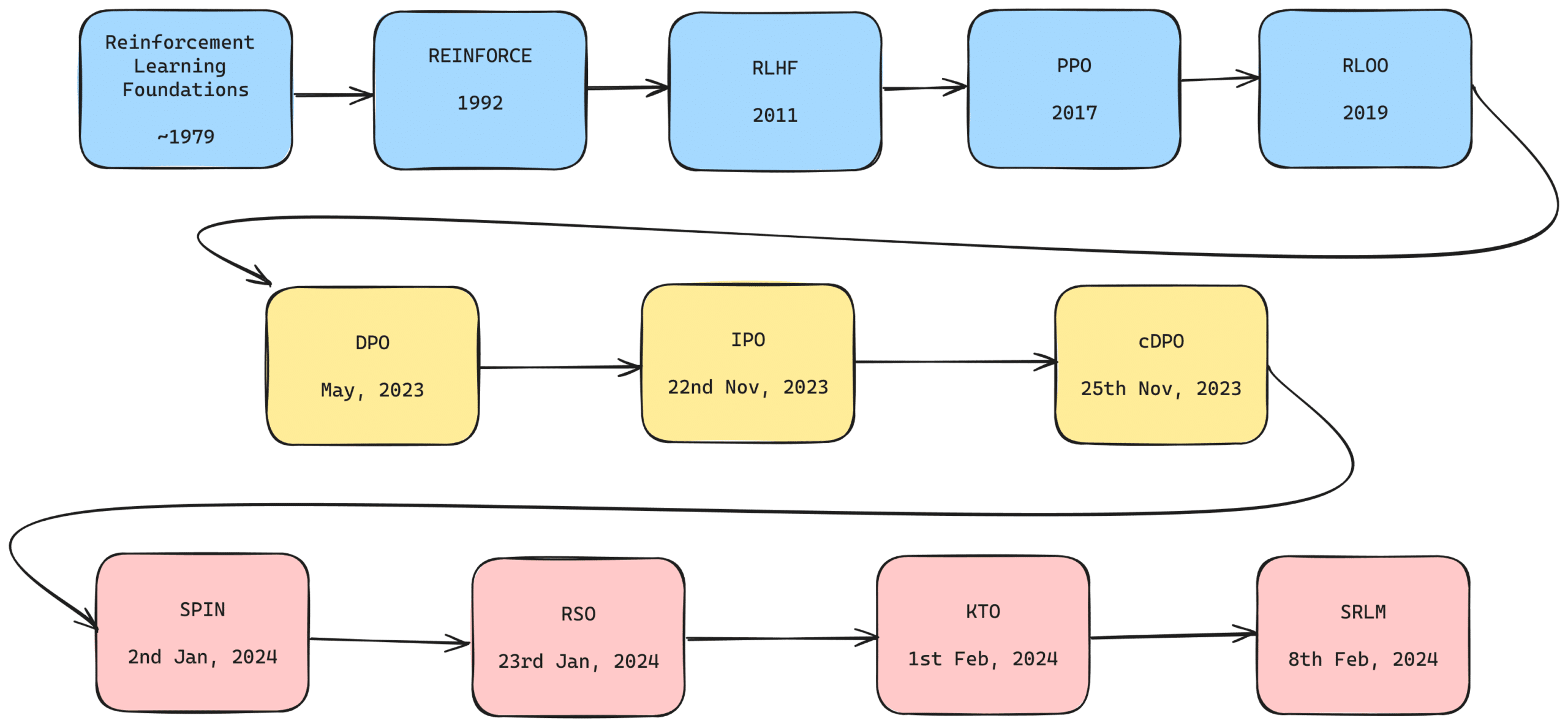
This field is in a constant state of evolution, with new algorithms continually being crafted to boost its efficacy. This comprehensive blog post will delve into these policy optimisation algorithms, exploring their strengths and limitations.

 

Note: In this article, methodologies establishing a foundational reward system are referred to as ‘algorithms,’ whereas the methodologies that employ these algorithms are termed ‘frameworks.’ It should be understood that these ‘algorithms’ may likewise operate autonomously as frameworks. However, for the sake of clarity and to delineate between the two modalities discussed herein, such terminological distinctions have been adopted.

Part A: Policy Optimisation Algorithms

RLHF and PPO

Our exploration of policy optimisation algorithms begins with an innovative solution named Reinforcement Learning with Human Feedback (RLHF). This technique ingeniously combines traditional reinforcement learning with human feedback. It functions by training a reward model based on human comparisons of different trajectories, which is then used to guide the agent’s policy. This combination of human intuition and machine learning has been successful in solving complex tasks that are beyond the reach of simple reward functions.

 

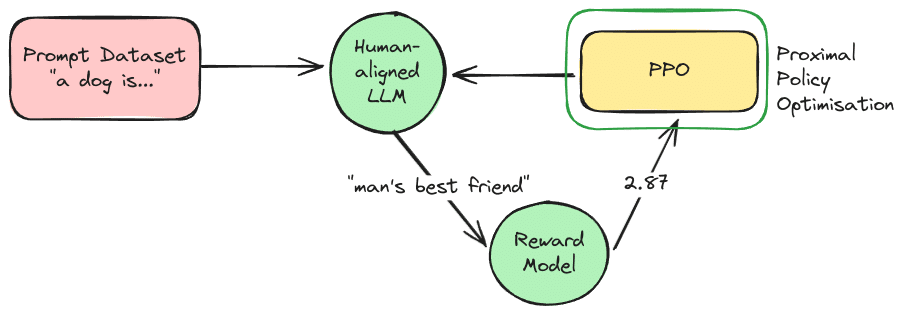
Notably, RLHF in OpenAI’s ChatGPT makes use of Proximal Policy Optimisation (PPO), a method developed by OpenAI itself. PPO is integral to the operation of RLHF as it helps in achieving a delicate balance between sample complexity and computational complexity. It employs a surrogate objective function to enhance the policy while ensuring that the updated policy doesn’t deviate significantly from the current policy. This balance allows PPO, and by extension RLHF, to make considerable progress during optimisation without risking harmful updates.

An In-depth Look at PPO (Proximal Policy Optimisation)

Unlike popular reinforcement learning approaches such as Deep Q-Networks (DQN) that can learn from stored offline data, PPO learns online. This implies that it does not rely on a replay buffer to store past experiences; instead, it learns directly from the interactions its agent has with the environment. Once a batch of experience is utilised for a gradient update, it is discarded, and the policy progresses forward.

One key distinction between policy gradient methods like PPO and Q-learning methods lies in their sample efficiency. Policy gradient methods tend to be less sample efficient since they utilise collected experience only once for each update iteration. Despite this drawback, policy gradient methods offer unique advantages and play an essential role in reinforcement learning algorithms’ landscape.

The loss function of PPO looks something like this:

 

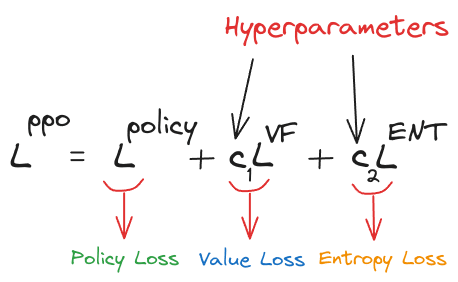
Breaking it down to better understand it:

1. The first term is the policy gradient loss, which maximises the probability of taking good actions. It’s calculated by comparing the new policy ($π$) to the old policy ($π_o$) using importance sampling, and is clipped to ensure that updates remain close to the original policy. The clip function helps in controlling the step size of updates hence preventing large updates that could hurt the performance of the agent, thus ensuring the “proximal” policy optimisation.
   1. The policy loss is given by $E[min(rₜ(θ)Aₜ, clip(rₜ(θ), 1-ε, 1+ε)Aₜ)]$
      • $rₜ(θ)$ is the ratio of the probabilities according to the new and old policies,
      • $Aₜ$ is the advantage function that indicates how much better an action is compared to the average of all actions,
      • $ε$ is a hyper-parameter that controls the degree of trust region in PPO
2. The second term is the value function loss (squared error loss) which minimises the error in value estimation. The value function predicts the future reward from a state, leading to better decision making by the agent.
   1. The value loss is given by $c_1*E_t[(V_w(s_t) – V_t)^2]$, ******where:
      • $V_w(s_t)$ is the estimated ‘value’ of the current state,
      • $V_t$ is the observed return
3. The third term is the entropy bonus, which encourages exploration by adding a bonus for more random policies. The entropy of a policy is a measure of its randomness. It is used to improve exploration by discouraging premature convergence to a sub-optimal policy.
   1. The entropy loss is given by $c_2E_t[Sπ_θ]$,* where:
      • $Sπ_θ$ is the entropy bonus which is a measure of the randomness of the policy

Limitations of PPO and Introduction of RLHF with DPO

While the reinforcement learning with human feedback (RLHF) framework has become a popular method for efficiently fine-tuning large language models to achieve downstream tasks, one major issue of this approach is its expensive computational cost. RLHF fine-tunes language models by leveraging human feedback to train a reward model, which then guides the language model towards generating preferred responses. This four-step process, although effective, grapples with challenges such as the need for large-scale reward models equivalent to the original model, leading to significant computational demands.

To address the computational requirement of RLHF and PPO, we can move to a newer method called Direct Preference Optimisation or DPO for short. The brilliance of DPO lies in its simplicity and directness. It bypasses the complexities inherent to RLHF by eliminating the need for a reward model. In DPO, human evaluators directly influence the model’s learning process by indicating preferred responses. The language model then utilises these indications to adjust its outputs, aspiring to maximise the likelihood of generating the favoured responses. This method not only simplifies the training process but also enhances stability and reduces computational overhead.

An In-depth Look at DPO Loss

In essence, this approach adopts a sophisticated two-pronged framework involving both an active ‘policy’ version of a language processing algorithm and its static counterpart or ‘reference’ version. During its enhancement phase—or training—the primary focus lies in fine-tuning this algorithm so it becomes more adept at identifying favourable responses over less ideal ones through comparative analysis against its reference iteration. This differential reinforcement not only streamlines improvements but does so by directly incorporating feedback mechanisms inherent within large-scale language models themselves.

This innovative utilisation of binary cross-entropy measures alongside strategic constraints like Kullback-Leibler divergence enables precise refinement without necessitating wide-ranging exploratory data evaluations or complex adjustments to operational variables—a common requirement in traditional optimisation methods. It paves way for methodical enhancements that maintain fidelity to original design intentions whilst elevating overall effectiveness significantly yet sustainably; all achieved with lesser demand on computational assets.

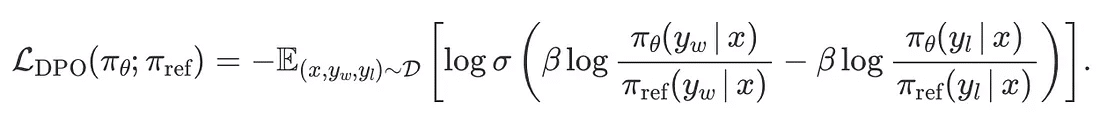
Let us break down this equation to understand what exactly is going on here:

• At the outset, let us focus on the sigmoid function’s constituents:
  • These elements are bound by a KL (Kullback-Leibler) divergence constraint comparing the logits generated by our model to those of a reference framework.
  • Additionally, they introduce penalties ensuring that the probability distribution produced by our model for an input $x$ more closely aligns with that associated with a ‘winning’ or preferred outcome $y_w$ as opposed to a ‘losing’ or less favoured one $y_l$.
  • This configuration stems from an ambition to optimise both a reward mechanism and a penalty derived from KL divergence. The formula for calculating rewards manifests in these specific terms.
• The presence of the sigmoid function is attributed to its application within the Bradley-Terry (BT) preference modelling framework. Herein, each generation’s reward is equated to its perceived ‘strength’.of
• By substituting computed reward values back into our model, we ascertain the likelihood that favourable outcomes possess greater ‘strength’ compared to their unfavourable counterparts.
• Converting this probability into logits via logarithmic transformation results in the bracketed expression. Given its statistical nature, it becomes essential to calculate this term’s expected value across dataset samples—an objective achieved through maximisation.
• Consequently, minimising its negative transforms it into an effective loss metric.

Limitations of DPO and Introduction of KTO, RSO, cDPO, and IPO

While DPO is a massive step forward towards lowering the entry barrier towards model alignment and model improvements, it still has some downsides to it:

1. Requirement of Paired Preference Data: A fundamental limitation of DPO is its need for paired preference data to function effectively. This constraint makes its application challenging in real-world scenarios where such specific pairs of preferences may not be readily available or easy to generate.
2. Noise Sensitivity: DPO is unable to deal with noise – specifically the chance of labels being incorrectly flipped with a small probability. This sensitivity to noise indicates a limitation in scenarios where data is imperfect or where there’s inherent uncertainty in preference expressions as is the case in the real world.
3. Inability to Sample Preference Pairs from the Optimal Policy: DPO struggles with sourcing accurate preference pairs due to the lack of a reward model. This limitation hampers its effectiveness in optimising policies that align with desired outcomes.

These limitations in data requirement and noise sensitivity are addressed by newer methodologies like KTO (Kahneman-Tversky Optimisation), RSO (Rejection Sampling Optimisation), IPO (Identity ‘phi’ Policy Optimisation), and cDPO (conservative DPO) which are designed to address some of these issues directly.

• KTO is an advanced method designed to enhance the utility of outputs by focusing on direct maximisation rather than relying on the log-likelihood of preferences.
  • This approach circumvents the need for paired preference data, streamlining its application in real-world scenarios where such data may be scarce. KTO utilises a modified Kahneman-Tversky value function tailored for large language models (LLMs), employing hyperparameters to distinguish between desirable and undesirable examples.
  • It also employs KL divergence estimation for optimisation purposes. Empirical evidence indicates that KTO performs competitively or even outperforms Direct Policy Optimisation (DPO) across various model scales without necessitating supervised fine-tuning or preference pairs, marking a substantial advancement over DPO, particularly in practical settings.

• RSO has been developed to mitigate DPO’s inability to sample preference pairs from an optimal policy due to the lack of a reward model. RSO employs statistical rejection sampling to more accurately derive preference data from an estimated target optimal policy.
  • RSO introduces an enhanced framework that refines loss functions previously used in SLiC and DPO, integrating a statistical rejection sampling algorithm for better optimal policy estimation. This involves complex mathematical modelling with techniques like logistic regression for DPO and support vector machine methods for SLiC, all optimised within the RSO framework.
  • Through rigorous testing, RSO has proven superior to both SLiC and DPO across diverse tasks, delivering marked improvements in aligning with human preferences as judged by top-tier LLMs and human evaluators. The research paper provides detailed insights into RSO’s methodology and its successful experimental outcomes.

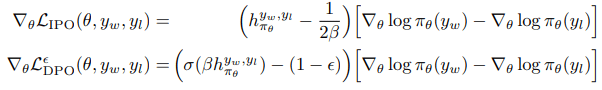
• Eric Mitchell‘s analysis sheds light on Direct Policy Optimisation’s loss function concerning current policy $π_E$, which expresses a preference $y_w$ over $y_l$ despite potential noise-induced label inaccuracies occurring with probability ε within 0 to 0.5 range.
  • The gradient of this loss function is computed as a weighted sum of two gradients based on ε values, achieving equilibrium when the estimated probability matches the desired confidence level under the Bradley-Terry model.
  • In contrast to standard DPO’s perpetual gradient descent, cDPO and IPO introduce specific enhancements targeting conservative updates; cDPO amplifies implicit probability assignments for observed preferences until reaching a predetermined threshold while IPO focuses on incremental implicit reward improvements up to a set point.
  • Both frameworks incorporate mechanisms that prevent or reverse optimisation if it deviates significantly from a reference model—a strategy that contributes to improved stability after prolonged training compared to traditional DPO methods.

Mimicking Human-Level Performance with SPIN (Self-Play fIne-tuNing)

The Self-Play fIne-tuNing (SPIN) methodology presents a transformative approach to enhancing Large Language Models (LLMs) by addressing the persistent challenge of data scarcity. SPIN employs a self-generated training mechanism, distinguishing itself as an efficient solution in scenarios where acquiring new data is impractical or expensive.

At its core, SPIN operates on the principle of self-play, where the LLM competes against previous versions of itself. This innovative technique allows the model to autonomously produce its own training material, thereby circumventing the limitations imposed by data unavailability. It draws parallels with Generative Adversarial Networks (GANs), but with a unique twist: the LLM’s adversary is its own historical iterations.

• The sophistication of SPIN lies in its ability to refine and enhance an LLM through Supervised Fine-Tuning (SFT), leveraging existing human-annotated data without necessitating additional resources.
• The process begins with a base model that has undergone SFT and progresses through iterative self-play. During this phase, the LLM generates responses based on past iterations and compares them to those derived from human annotations. Through this comparison, it incrementally improves its policies, aligning more closely with the desired target data distribution.
• The loss function is formulated through adversarial calculations, where the previous model attempts to deceive the current model into misclassifying synthetic data as genuine. Conversely, the current model functions as a discriminator, discerning between real and generated data. The objective is to identify a function that amplifies the discrepancy between these two data types. The generator aims to align with a probability distribution that elevates this function’s output, thereby narrowing the gap with authentic data. A Kullback-Leibler (KL) divergence term is incorporated to restrain significant deviations from the antecedent model. Through strategic adjustments, we can derive the loss function that the discriminator endeavours to minimise for optimal performance.

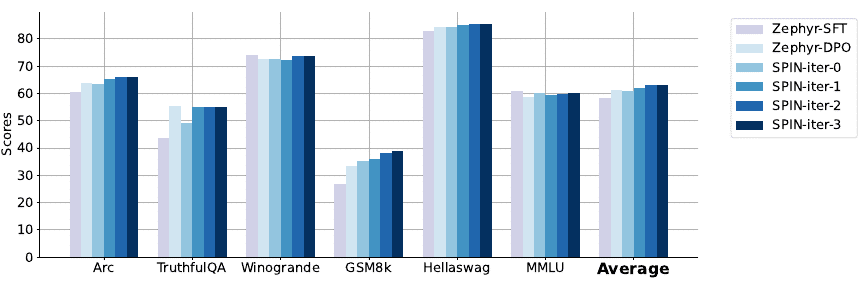
The efficacy of SPIN has been proven through theoretical analysis and empirical testing. Theoretical proofs confirm that optimal training outcomes are achieved when the LLM’s policy is congruent with the target distribution. Empirical assessments conducted on various benchmark datasets—including those from HuggingFace Open LLM Leaderboard, MT-Bench, and Big-Bench—demonstrate SPIN’s capacity to significantly boost performance metrics across diverse benchmarks.

Remarkably, these advancements have been realised without resorting to Direct Preference Optimisation (DPO) strategies or relying on supplementary GPT-4 preference data. Instead, SPIN’s self-sustaining nature fosters continuous improvement within the LLM framework, propelling it towards achieving human-level proficiency.

SPIN represents a leap forward for LLM development by utilising a self-reinforcing cycle of learning that exploits existing annotated datasets to their fullest potential. This method not only optimises resource utilsation but also sets a precedent for achieving superior language model performance through strategic self-play dynamics.

Back to REINFORCE with REINFORCE Leave One Out

A recent study titled “Back to Basics: Revisiting REINFORCE Style Optimisation for Learning from Human Feedback in LLMs” from Cohere AI challenges the status quo of PPO being held as the champion for efficiency by advocating for a preexisting, simpler, more efficient method derived from the REINFORCE algorithm and its multi-sample extension, REINFORCE Leave-One-Out (RLOO).

The study employs two primary datasets: the TL;DR Summarise dataset and the preprocessed Anthropic Helpful and Harmless Dialogue dataset. The Pythia-6.9B model serves as the base for these datasets, with experiments also conducted using Llama-7B to assess the impact of pre-trained model quality. The authors ensure a consistent experimental setup across all methods by maintaining a fixed context length and initialising both the reward model and policy with the corresponding Supervised Fine-tuning (SFT) checkpoint.

The study finds that:

1. REINFORCE-style methods, particularly RLOO, not only simplify the policy optimisation process but also outperform traditional approaches like PPO and recent RL-free methods such as DPO and RAFT. RLOO consistently outperforms other methods in reward optimisation, showcasing its efficacy in aligning models to human preferences with greater sample efficiency.
2. RLOO’s superiority in utilising generated samples for optimisation underscores a significant advantage over more complex methods. By effectively leveraging all samples generated, RLOO showcases enhanced optimisation capabilities with fewer resources, making it a compelling choice for RLHF tasks.
3. The robustness of RLOO against variations in KL penalty and reward noise further strengthens its case. It maintains better reward optimisation and exhibits less deviation from the reference policy under varying conditions, showcasing its resilience and reliability in real-world applications.

The findings from this study underscore a pivotal shift towards simplifying the RLHF landscape. By revisiting the fundamentals through REINFORCE and its extension, RLOO, the study not only challenges the prevailing dominance of PPO but also presents a compelling argument for the broader applicability and effectiveness of simpler, more efficient methods in optimising policy objectives for LLMs. This exploration into REINFORCE-style optimisation methods marks an opening of newer avenues for research and application in the field of machine learning and beyond.

Part B: The Policy Optimisation Frameworks

Self Rewarding Language Models

The effectiveness of current methodologies in machine learning is often hampered by the limited quantity and quality of data reflecting human preferences. Reinforcement Learning from Human Feedback (RLHF) faces a particular challenge: once its reward model is trained, it becomes static and does not benefit from further refinements to the primary Large Language Model (LLM).

To address these limitations, researchers at Meta have proposed an innovative approach known as Self-Rewarding Language Models (SRLMs). A recent study highlights that this strategy involves developing an agent that integrates all necessary functions during its training stage, thus obviating the need for distinct reward and language models.

This novel model employs AI Feedback (AIF) to continuously enhance itself via self-directed training iterations. Each cycle results in the model’s improved proficiency in interpreting instructions and generating high-quality training examples for subsequent cycles.

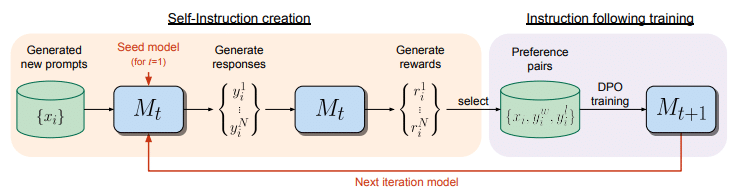
The process begins with a foundational LLM extensively trained on a broad corpus of text. This base model undergoes refinement through a small set of carefully selected human-annotated examples or seed data. This includes instruction fine-tuning (IFT) examples comprising pairs of instructions and their corresponding responses.

Additionally, to boost the model’s efficacy, evaluation fine-tuning (EFT) examples are used. Here, the LLM is tasked with ranking multiple responses based on their relevance to an instruction prompt, providing detailed explanations and scores for each response. These EFT instances enable the LLM to perform as both language and reward models.

Following this initial training on seed data, the model can autonomously generate new instructional materials for future training rounds. It selects from IFT samples to create fresh prompts and produces various potential answers for each one.

Review the user’s question and the corresponding response using the additive 5-point scoring system described below. Points are accumulated based on the satisfaction of each criterion:
- Add 1 point if the response is relevant and provides some information related to the user’s inquiry, even if it is incomplete or contains some irrelevant content.
- Add another point if the response addresses a substantial portion of the user’s question, but does not completely resolve the query or provide a direct answer.
- Award a third point if the response answers the basic elements of the user’s question in a useful way, regardless of whether it seems to have been written by an AI Assistant or if it has elements typically found in blogs or search results.
- Grant a fourth point if the response is clearly written from an AI Assistant’s perspective, addressing the user’s question directly and comprehensively, and is well-organized and helpful, even if there is slight room for improvement in clarity, conciseness or focus.
- Bestow a fifth point for a response that is impeccably tailored to the user’s question by an AI Assistant, without extraneous information, reflecting expert knowledge, and demonstrating a high-quality, engaging, and insightful answer.
User:
After examining the user’s instruction and the response:
- Briefly justify your total score, up to 100 words.
- Conclude with the score using the format: “Score: ”
Remember to assess from the AI Assistant perspective, utilizing web search knowledge as necessary. To evaluate the response in alignment with this additive scoring model, we’ll systematically attribute points based on the outlined criteria.

A critical component is the ‘LLM-as-a-Judge’ phase where the model evaluates these candidate responses using specialised chain-of-thought style prompts that include original requests, potential answers, and criteria for effective assessment. Through such iterative self-improvement using internally generated content judged by its own standards, the language model increasingly hones its understanding and response capabilities.

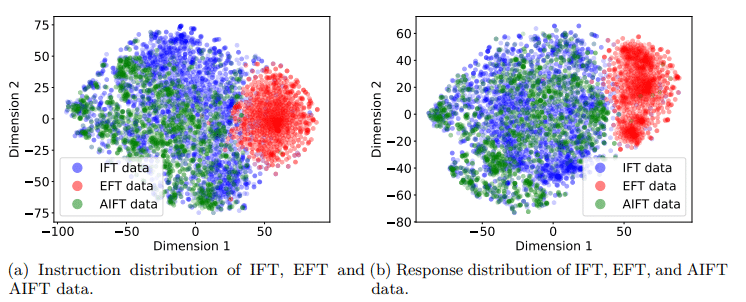
Once it has crafted instructional examples and assessed responses, SRLM utilises them to compile an AI Feedback Training (AIFT) dataset. There are two approaches to constructing this dataset: one can combine instructions with responses and ranking scores to form a preference dataset—used alongside direct preference optimisation (DPO)—to teach the model discernment between high-quality and subpar responses; alternatively, one can create a supervised fine-tuning (SFT) dataset featuring only top-ranked responses. Research indicates that including ranking information enhances trained models’ performance. They also found that IFT data and EFT data come from very different distributions while the IFT and AIFT(M1) data come from similar distributions which is the exact objective of generating data that mimics the original distribution.

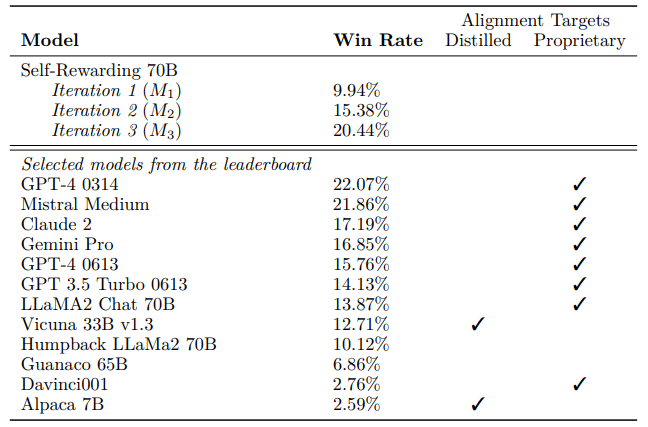
The research team conducted experiments with self-rewarding language models (SRLM), using the Llama-2-70B as the foundational model. They utilised the Open Assistant dataset for instruction fine-tuning, which includes a plethora of examples specifically designed for this purpose. This dataset also offers instruction sets paired with ranked responses, suitable for evaluation fine-tuning (EFT).

Results indicate that each SRLM iteration enhances the language model’s capacity to follow instructions and refine its reward modelling. This cyclical improvement facilitates the generation of superior training samples in subsequent iterations. In comparative tests using the AlpacaEval benchmark, Llama-2, after three SRLM iterations, surpassed Claude 2, Gemini Pro, and GPT-4-0613.

However, this method has its constraints. Similar to other self-improvement techniques for large language models (LLMs), there is a risk of “reward hacking,” where models erroneously optimise for expected outcomes. Such pitfalls can yield unstable models ill-suited for real-world tasks divergent from their training data. The scalability of SRLM concerning model size and iteration count remains uncertain.

Nevertheless, SRLM presents a distinct advantage by amplifying an LLM’s capabilities using existing datasets without necessitating additional examples—thereby maximising training data efficiency. By incorporating these newly minted examples into the original dataset for retraining purposes, this recursive process begets progressively more competent models in both executing instructions accurately and evaluating responses effectively.

Direct Preference Feedback (DPF)

In the fast-evolving domain of language models, the “Pink Elephant Problem,” where models inadvertently focus on undesired topics, presents a significant challenge. A recent paper introduces an innovative solution: Direct Principle Feedback (DPF). This technique simplifies and refines the Reinforcement Learning from AI Feedback (RLAIF) process, enabling language models to be controlled at inference time for more desirable conversational outcomes, steering clear of “Pink Elephants” and towards “Grey Elephants.”

DPF simplifies traditional language model training by directly applying critiques and revisions, weaving them into the fine-tuning phase. This contrasts with the more complex RLAIF approach. The conventional RLAIF method proposed by Bai et al.(2022b) involves:

1. Fine-tuning models on examples with critiques.
2. Further revisions followed by fine-tuning a new model.
3. Generating responses and ranking them by human or AI.
4. Utilising algorithms like PPO or DPO to refine the model.

DPF collapses this multi-step approach into a single streamlined step. It leverages natural response-revision pairings to instil behavioural guidelines, bypassing the need to rank outputs for conformity to desired behaviours. This makes DPF exceptionally effective for tasks such as avoiding certain topics dynamically at inference time.

The effectiveness of DPF is further elucidated through empirical evidence, where it surpasses both baselines and GPT-4 in guiding conversations away from Pink Elephants. The OpenHermes-7B and OpenHermes-13B models, for instance, showed notable improvements with the implementation of DPF. Here’s a snapshot of their performance enhancements:

• OpenHermes-7B with DPF: Showed performance enhancement from a base rate of 0.33 to 0.36 without CFG, and 0.17 with CFG, reflecting DPF’s impact.
• OpenHermes-13B with DPF: Maintained a base rate of 0.34, with a notable improvement to 0.15 when combined with CFG.
• GPT-4: Demonstrated a substantial performance leap from a base rate of 0.33 to 0.13 with the aid of DPF.

These improvements emphasise DPF’s potential in effectively redirecting language model outputs towards preferred topics and behaviours at inference time.

Conclusion

Policy optimisation algorithms stand tall as the pivotal pillar holding up the mechanism of reinforcement learning. Over the course of the years, these algorithms have seen a remarkable evolution, each new development and method aiming to address and rectify the shortcomings of its predecessor. This journey of growth and evolution has led to the emergence of an array of impactful methods. From the application of RLHF using PPO (Proximal Policy Optimisation) and DPO (Distributed Proximal Policy Optimisation), to the breakthrough of RLAIF (Reinforcement Learning with Augmented Inference Frameworks) in the innovative form of Self-Play Fine Tuning (SPIN) and Self Rewarding Models (SRMs), each advancement has made significant strides in augmenting the effectiveness of reinforcement learning methodologies. As this dynamic and ever-evolving field continues to expand its horizons, it paves the way for a fascinating future. It beckons one to watch eagerly as it promises to deliver new developments and advancements that lie waiting to be discovered in the road ahead.